Happy accidents

I've been teaching for a good while now, but I'm happy to know that there are still things I can learn, because it keeps me sharp. Also? Happy accidents become teachable moments and an exercise for one class turns into several exercises for three different classes.

I'm always on the lookout for "real-world" examples of math and physics that aren't the usual boring cell phone/well bore/cannon ball stuff. I came across this video of the water fountain at Detroit International Airport and was struck by one image that was filled with different parabolas, thanks to the initial velocity of the water and the perspective of the shot. I turned it into an exercise and assignment for my MCR3U where they had to find the equations of two parabolas, and then the equation of three lines, one which was a secant to one parabola, one which was a tangent to the other, and the third was a secant to one and a tangent to the other.

Naturally, I wanted to modify it for use with my MCF3M class. I came up with an exercise where they find the equations of two parabolas: one in root form and one in vertex form. For their assignment, they'll have to turn each equation into the other form algebraically (plus standard form for good measure).

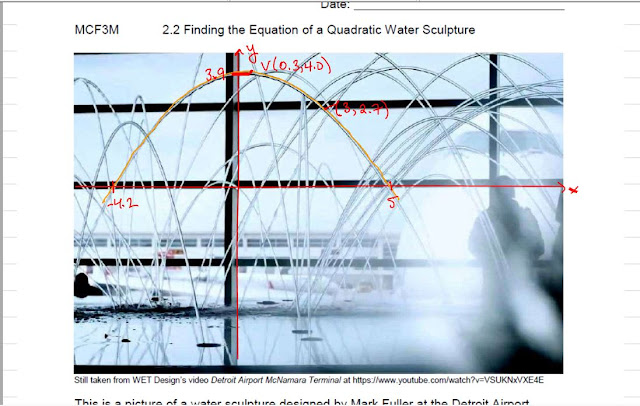
I tried it out three days ago. To help them prep, I got them to pick the axes and a parabola to look at (noting that each water jet is actually two parabolas). We measured the roots and used the y-intercept to find the a value. Pretty straightforward, and I thought determining the vertex form would be a snap.

Except that when we calculated a, we got a completely different number. Not "we're off by a few decimal places" different, but -0.19 vs -1.1 different. These students are still struggling a bit with vertical stretches and compressions, so a discrepancy like that is not on. 

I asked a colleague to verify my calculations, and he figured out that my calculations were fine. The problem was probably that for the parabola the class chose, the y-intercept and vertex were so close together that a=-1.1 was within the accepted error. I used another point far from the vertex and got a=-0.18. Much better.

[By the way, we I did also make some heinous measurement and calculation mistakes, but since all mistakes I make are intentional (ahem), this just gives me an opportunity to talk about making sure our values make sense. More happy accidents.]

Unfortunately, I had the DLL PD today, so I wrote this all down on the board and hope they got it during today's class. I'll review on Friday when I next see them. They need to have the equations (and domains and ranges) ready for next Thursday's assignment.

That discrepancy is really interesting. I will have to modify this worksheet to tell the students to make sure their points are not too close together. Plus, I may have accidentally stumbled on a realistic way to teach uncertainty in my grade 11 physics class. A happy accident indeed. I'll keep you posted.

Once I get my act together, I'll create a page where I will share my various worksheets and handouts. For now, check out my course webpages (link up top) under "Handouts and Assignments". My class notes for both (all three?) lessons will be posted under the "Notes" section at the end of the month.